回覆Gilbert
有關數學字母及運算符號使用的是html語法中Latex程式碼。舉例來說:在發表新文章的時候,編輯區右上角點選修改HTML,就會顯示HTML碼,打上
<img src="http://www.codecogs.com/eq.latex?\frac{3}{2}" />,再點選右上角撰寫,就會顯示出
PS:在意見欄中無法讀取<img src="http://www.codecogs.com/eq.latex?\frac{3}{2}" />,所以以新文章發佈
中華白海豚
四點共圓的行列式判別法
四點
說明:設四點
則A、B、C、D皆滿足此方程式
讓
必有解(
因此根據克拉瑪公式
同樣的方法亦可使用在空間中四點
至於四階行列式怎麼算呢?就要先降成三階再來算,請自行上網查詢。
[Chemistry]溶解度的影響因素
濃度低於飽和溶液的為未飽和溶液,濃度高於飽和溶液的為過飽和溶液
以上三項定義就像幾何學的公設,關於溶解現象的討論需要建立在關於濃度的分類上
1.物理條件:溫度、壓力(氣體而言),為所謂環境的部份
2.化學條件:溶劑、其他溶質的種類和濃度,某些特定離子的濃度可視為環境的一部分,
水溶液中的平衡
就水溶液而言,其化學方程式可寫成如下形式
藉由方程式,我們就能將溶解度變化轉成反應趨勢,也就是勒沙特烈原理的運用
影響溶解度的所有條件都能分配至方程式的兩邊,方程式兩邊的項也能代表特定的條件
兩者是互為充要條件的。利用方程式可以預測環境變化對溶解度的影響。
空間之線段和最小值求法
所以小弟我就在以下PO上個人淺見,
四點共圓
前幾天帥氣中右葛問到說,
「如果我知道四個點的座標,有什麼方法可以判斷四點共圓?」
小弟我在這裡稍微題一下一些常用的四點共圓的特性。
1.多點共圓的基本定義
平面上有n個相異點A1~An,且有一點A0使得A0A1=A0A2=......=A0An, 即A1~An到A0的距離皆相同,則A1~An共圓,且圓心為A0。 基本的多點共圓的定義,在一般的歐氏幾何證明中常常運用的基本定義。
這個方法可以搭配解析幾何,利用很刺激的方式先炸出其中三點的外接圓式子再把其他點帶入計算......很刺激囉XD
2.利用圓的基本性質
像是大家應該都還記得的「圓內接四邊形對角互補」,「圓周角=PI/2」,這類的東西,這些東西在國中應該都有聽老師提過了,其實國中教的幾何 還真是超級重要啊XD
3.利用Ptolomy(托勒密)定理
對於任意的四邊形ABCD,有AB*CD+BC*DA ≧ AC*BD。 "="成立於ABCD四點共圓,此時即為常見的Ptolomy定理,可以利用長度的一個關係判斷四點共圓。
4.利用Simson(西摩松)定理
給定一個三角形ABC,以及三角形外一點P。若P對AB.BC.CA三邊的垂足三點共線,則ABCP四點共圓。
在知道AB.BC.CA三直線方程式和P點座標的時候應該還算可以用的東西。當然如果直線方程式係數不要太難看,可以解交點代Ptolomy是 不錯的選擇。
Simson的話可能就是考慮在知道投影點(垂足)的情況下用用看囉XD 這個算是比較冷門的定理了這樣。((倒是有用這個定理把學科的幾何題目秒殺過就是,97年第6區數學科第一試第一題XD))
證明四點共圓的方法有很多,後面兩項利用定理的方法只是方便一點而已。
真正重要的是利用基本的定義、性質去解讀題目給的東西。
雖然現在在學解析幾何,不過基本的定值還是要記得XD
解析幾何只是工具幫助分析而已。
植物的繁殖
1.世代交替
這個是植物界生物都有的現象,但並不僅限植物界生物才有!! ←(關於例外會再行補充)
所謂世代交替,就是指在生活史中,植物交替出現
※孢子體世代(2n):由配子發育而成,最終將製造(減數分裂)出孢子(1n)
※及配子體世代(1n):由雌雄孢子各自發育(有絲分裂)而成,成熟後各自製造出雌雄配子進行精卵結合,形成合子發育為孢子體。
※另外,配子體在蘚苔植物顯著,在蕨類植物可獨立生存(但小片),從裸子植物開始即不可獨立生存。 ←(另外再詳述)
2.無性生殖
簡言之,不用經過整個生長週期就能產生新個體
常見的方法有營養器官繁殖、組織培養
※營養繁殖:某些植物的營養器官可以直接發育成為新植株,
※插枝:某些植物適合插枝繁殖,通常剪下年輕的枝條並修去較下端(老葉)的葉子進行培養
ex:黃金葛
※組織培養:將植物組織取下一小部份,放入消毒過的培養基後加入適當物質(包括IAA、CK等)便可培養出整顆植株
※其餘較少見的壓條、扦插再另行補充
3.(終於要進入的)有性生殖
我們將植物界(從蘚苔類開始)的植物稱為胚胎植物,這是因為他們的合子(人類的受精卵)形成後都會在母體上發育成胚,然後才脫離母體
※胚:由合子有絲分裂而來,在被子植物中包含子葉、胚芽、胚軸、胚根 ←(小心,相當常考)
※演進:
蕨類植物→兩世代皆可獨立生存 →孢子體發達
裸子植物→演化出胚珠、花粉,不需水完成授精 →孢子體發達
被子植物→演化出花的構造,具雙重授精 →孢子體發達
※演化方向:趨向孢子體發達
原因:孢子體是具有2n的世代,並可行減數分裂,在遺傳變異上的助益較大
[Physics]多質點系統動力學
基於和上次 有部分是相同的,一開始便放一些上次的東西
另外,肥某,某閔,像小弟我反映說看不懂積分符號,其實寫那個只是想讓對物理有興趣的人看的,把握關鍵性的觀念比較重要
這次先發觀念,下次在大概談些解題技巧,如果大家有不懂的問題,可以再討論區提出,小弟儘可能的幫大家解決。
對於多個質點來說,我們可以以類似力矩的手法求出質心的位置,下面先假設有n個質點,第n個質點的質量為Mn,具原點的距離為Xn。則質心位置可有以下的表示法。一般來說原點可以任意取,方便計算即可。
上面是分布在一維空間的情況,我們可以用相同的手法推展到三維空間,甚至可以用向量來定義質心。此外一般的固體可以將其質量是為連續分布,而質點就是微小的質量素dm,累加起來便形成了以積分定義的方式。
現在如果將上式,對時間微分的話,位置對時間微分叫速度,則質量與速度之乘積,就是動量,因此變成下式。這便是所謂的動量守恆,質心動量等於質點系統的總動量。
如果比較4、5兩式,不難發現
這告訴我們,質點系統中,各質點對質心的動量和為零,也就是"內動量"等於零。
因此,在解題時,有時將原點取在質心,可以大幅簡化問題。
再來就像推導4式的方法,如果我們將3式對時間做兩次微分,可得到下式,這個式子的意義在於:質心的運動方式就好像我們將各質點所受的力全部搬到質心上。
值得注意的是,上式寫的是受力,那如果各質點也有交互作用力呢?一般而言,各質點的交互作用力稱做"內力",根據牛頓第三運動定律,可得到內力之合會等於零(詳細推導過程這裡就不列出),因此:質心的運動方式就好像我們將各質點所受的外力全部搬到質心上,善用此一技巧亦可,簡化問題。
[Math]數學介紹文 - 空間幾何基本概念
什麼叫做幾何呢?
其實我是上了劉輝老師的課才在想這個問題((笑)),
在平面幾何中,討論的是點與線的關係;
在空間幾何中,討論的是點線面的關係。
也就是說幾何是在討論點線面三者之間的關係的學問。
當然啦,
要把點改成喵,線改成汪,面改成嘓也是無所謂的((只是沒人那麼叫
重點是在這三個傢伙之間的關係總而言之啦這樣=w=
那麼就來進入主題吧。
重要基本公設:
不共線三點決定一平面
其實後面導出的很多決定平面的方法都是要依據這條公設的前提來提出的,
所以如果沒有背哪些情況可以決定一個平面的話,
直接判斷是不是有固定的不共線三點就可以了。
裡面提到了公設嘛,
所謂的公設就是那些不用證明的事情,
像是還有兩個點可以決定一直線之類的。
((詳細再看看有沒有心情來Po幾何原本的介紹文好了,
後來很多公設都衍生出其他的非歐幾何(Ex黎曼.羅夫丘巴斯基的球面幾何),摁。))
關於這個公設的解釋,
什麼叫做不共線三點決定一平面呢?
我們想想看是不是有個傢伙叫三角形?
而且構成三角形的基本條件是三個不共線的點。
於是把三角形拉的很大很大就變成一個在空間中通稱的面啦=w=
((所謂空間中通稱的面就是代表著沒有邊際的面(亦可視邊界在無線遠處),而三角形是被約束的面這樣
點跟線的關係應該大家都不陌生,
所以這裡就不提了。
至於空間中線跟面的關係主要有以下:
((討論到面都是在空間中才會討論的
(1)線在平面上

(2)直線平行平面

(3)直線交平面於一點

目前為止的三種關係應該算是比較直觀明瞭的((相信我,讀幾何需要有直覺XD)),
那麼接下來是比較麻煩的垂直。
(4)直線垂直平面
圖上有一個平面,兩條平面上的直線,以及一條垂直的直線。
那麼為什麼要有那兩條直線,
實際上我們要有一直線垂直平面的話,
那條直線必須要同時垂直平面上兩條直線才可以。
((詳細說明等到後面三垂線定理在做詳細解釋
另外就是在空間中特別出現的一種線與線的關係,
(Special)歪斜線
在之前應該已經知道了同一平面中兩直線的關係,
重合、平行、相交一點。
平面中的兩直線必然有上面這三種關係的其中一種((三一律嗎?噢,這麼說好像也有道理XD
但是到了空間中就多了歪斜這種關係,
歪斜指的是,
空間中不共面的兩直線。
這跟平行不太一樣,
雖然都是不相交,
但是在還是在最關鍵的地方有致命的差別:有沒有共平面。
所謂的平行是指同一平面中不相交的兩直線,
但是歪斜是空間中不共面的兩直線喔。
那麼既然把幾何的維度進化到三維,
角度的討論當然也要從二維中兩直線的交角推廣到兩平線的交角囉=w=
((讀數學的人真是不得好死呢,你們是這麼想的嗎= =
面與面交角
用了三張圖來表示了面與面的交角,
課本說要找兩條分別為在兩平面上且垂直交線的直線,
如果換個角度想就是從可以把兩個平面當成兩條線的位置看的兩直線夾角,
就是從圖三的角度去看。
然後要找兩平面交角還是必須從定義去著手,
至於我的習慣讓兩平面上的兩條線在兩平面交線有共同垂足,
因為找角度就可以代餘弦啦~~這樣子。
((Ex圖一、二))
以上就把基本觀念介紹的差不多了,
那麼接下來就介紹很重要的定理,
三垂線定理
先從基本的兩個位置來看這個三垂線定理的圖,
一般在說明三垂線定理的時候啊,
都是說A對平面E做垂線,交於B點,
然後B再對直線L做垂線,交於C點,
之後可以得到AC垂直L。
說明:
已知AB垂直平面E,BC垂直直線L,證明AC垂直L。
在L上取一點異於C的點D,
我們要證明的就是AD2 = DC2 + AC2
隨後再根據畢氏定理逆定理即可((就是把畢氏定理反推過來想
證明:
DB2 = BC2 + CD2
= (AC2 - AB2) + CD2
=>DB2 + AB2 = AC2 + CD2
=> AD2 = AC2 + CD2 ((根據前面的基本介紹,因為AB垂直平面E,所以也垂直E上的任一條線,包括BD
所以AC垂直L
這是比較常見的三垂線定理,
事實上在這三段垂直中改變一下要證明的東西,
也是可以導出一樣的結果,
總而言之,
就是兩個垂直,則第三個也垂直。
有興趣的話就自行證明囉=)
那麼接下來換幾個角度來看這項定理。

上面這張圖主要強調的是AB垂直E的情形。
上面這張圖主要強調的是BC垂直於L的情形,
角度問題很抱歉@@

上面這張圖強調的就是AC垂直於L的情況。
特別把三條線段的垂情況提出來,
主要要強調的事情是投影這東西。
事實上把三垂線定理換個方式說明,
可以說成:
空間中平面E外一點A,
對E做一次投影,得其投影點B,
再用其投影點對直線L做二次投影C,
得到的二次投影點C和A直接對L做的投影點相同。
最後來利用三垂線定理解釋之前說為什麼直線垂直平面的條件是那條直線要同時垂之平面上兩直線。
看到AC線段和L線段,
AC垂直L,
但是能夠很直觀的發現AC不垂直平面E!
事實上過C點在E上畫其他直線都不會和AC垂直,
所以AC自然不會垂直E。
另外就是考慮說有一個平面F過C點垂直L、E
而AC只是這個平面F上的隨便一條線,
於是就不能保證AC垂直E囉這樣。
應用軟體:Cabri 3D v2

 1
1 2
2 3
3 4
4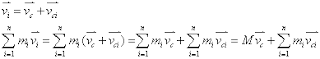 5
5 6
6 7
7







