今天來跟各位談談質點系統好了
基於和上次 有部分是相同的,一開始便放一些上次的東西
另外,肥某,某閔,像小弟我反映說看不懂積分符號,其實寫那個只是想讓對物理有興趣的人看的,把握關鍵性的觀念比較重要
這次先發觀念,下次在大概談些解題技巧,如果大家有不懂的問題,可以再討論區提出,小弟儘可能的幫大家解決。
對於多個質點來說,我們可以以類似力矩的手法求出質心的位置,下面先假設有n個質點,第n個質點的質量為Mn,具原點的距離為Xn。則質心位置可有以下的表示法。一般來說原點可以任意取,方便計算即可。
上面是分布在一維空間的情況,我們可以用相同的手法推展到三維空間,甚至可以用向量來定義質心。此外一般的固體可以將其質量是為連續分布,而質點就是微小的質量素dm,累加起來便形成了以積分定義的方式。
而其中重要的觀念是下面這個式子,M是總質量,rc是質心位置,及
各質點的質量與位置的乘積和等於總質量乘以質心位置。至於要如何應用來解題,就看r的向量要怎取,可以用直角坐標,或是單純就一個方向,如水平方向。(補充一點,質心位移也可以用這樣的表示法,將r都換成各自的位移即可)
現在如果將上式,對時間微分的話,位置對時間微分叫速度,則質量與速度之乘積,就是動量,因此變成下式。這便是所謂的動量守恆,
質心動量等於質點系統的總動量。
補充一點,如果將各自的速度,用向量分解的方式,寫成質心速度加質點對質心的相對速度,則可以得到下面的式子。
如果比較4、5兩式,不難發現
這告訴我們,
質點系統中,各質點對質心的動量和為零,也就是"內動量"等於零。
因此,在解題時,
有時將原點取在質心,可以大幅簡化問題。
再來就像推導
4式的方法,如果我們將
3式對時間做兩次微分,可得到下式,這個式子的意義在於:
質心的運動方式就好像我們將各質點所受的力全部搬到質心上。
值得注意的是,上式寫的是受力,那如果各質點也有交互作用力呢?一般而言,各質點的交互作用力稱做"內力",
根據牛頓第三運動定律,可得到內力之合會等於零(詳細推導過程這裡就不列出),因此:
質心的運動方式就好像我們將各質點所受的外力全部搬到質心上,善用此一技巧亦可,簡化問題。

 1
1 2
2 3
3 4
4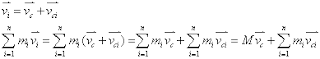 5
5 6
6 7
7